4. ケプラーの第3法則
調和の法則ともいいます。
「惑星の公転周期の2乗は、その惑星の太陽からの平均距離の3乗に比例する。」
公式で表すと以下のようになります。
$$T^2=kr^3$$
\(T\):惑星の公転周期、\(r\):惑星の太陽からの平均距離、\(k\):定数です。
惑星の太陽からの平均距離\(r\)は、楕円軌道では楕円の長半径と一致します。
定数\(k\)は、公転周期を「年」、距離を「天文単位(AU)」で表した場合、太陽系では1になります。
ちなみに天文単位とは、太陽と地球の平均距離を1AUとした距離の表し方です。
豆知識④ ニュートンの万有引力の法則による証明
ケプラーの第3法則は、ニュートンの万有引力の法則によって証明されます。
ここで質量\(m_{1}\)の物体と、質量\(m_{2}\)の物体の間にはたらく引力を考えます。
この2つの物体間の距離を\(r\)とすると、図3のような引力\(F\)がはたらきます。

図3. 2つの物体間にはたらく万有引力の図
引力\(F\)は以下の式で表すことができます。
$$F=\frac{Gm_{1}m_{2}}{r^2}$$
\(G\)は重力定数と呼ばれるもので、宇宙のどこでも一定の値です。
ここで、太陽のまわりを回る惑星を考えましょう。
太陽の質量を\(m_{1}\)、惑星の質量を\(m_{2}\)、惑星の公転周期を\(T\)とします。
話を単純にするために、ここでは惑星の軌道を半径\(r\)の真円としましょう。
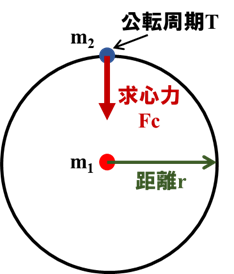
図4. 半径\(r\)の軌道をまわる惑星にはたらく力
公転する惑星には、常に太陽の方向に向けて「求心力」と呼ばれる力がはたらきます。
求心力\(F_{c}\)は、以下の式で表されます。
$$F_{c}=\frac{m_{2}v^2}{r}=\frac{4\pi^2m_{2}r}{T^2}$$
\(v\)は惑星が公転軌道上をすすむ速さで、軌道の長さ\(2\pi\)\(r\)を公転周期\(T\)で割ったものです。
この、求心力\(F_{c}\)が、引力\(F\)と等しくなります。
$$\frac{Gm_{1}m_{2}}{r^2}=\frac{4\pi^2m_{2}r}{T^2}$$
これを書き換えると、以下のようになります。
$$m_{1}=\frac{4\pi^2}{G}\frac{r^3}{T^2}$$
\(\frac{r^3}{T^2}\)の部分に着目してください。
\(m_{1}\)は太陽の質量なので、決まった値です。
すなわち、どの惑星についても\(\frac{r^3}{T^2}\)は等しい値でなくてはいけません。
よって、ケプラーの第3法則である、\(k=\frac{T^2}{r^3}\)(\(k\)は定数)が証明されました。
5. まとめ
ケプラーの法則は、とてもシンプルなものです。
しかしそれは、ヨハネス・ケプラーとティコ・ブラーエという2人の学者が、気の遠くなるほどの観測データを収集し、完成させたものです。
400年も昔に発見された法則が、現代の宇宙観測にも使われているのです。
.png)