潮汐力と聞くと、潮の満ち引きを思い浮かべる人が多いのではないかと思います。
しかし、潮汐力と潮汐現象(潮の満ち引き)は異なるもので、本来は別のものとして考えなくてはいけません。
潮汐力とは、「重力の影響下にある物体にかかる力」のことです。
それに対して、潮汐現象は「重力と遠心力の合力により引き起こされる海水の変化」です。
目次
1. 潮汐力とは何か
物体Yからの重力(万有引力)の影響を受けている物体Xを考えます。
ここで、2つの物体間にはたらく万有引力\(F\)についておさらいします。
詳しくは、『ケプラーの法則 ~惑星が回る軌道のお話』の記事に記載したものです。
万有引力\(F\)は以下の式で示されます。
$$F=\frac{Gm_{1}m_{2}}{r^2}$$
\(G\)は重力定数、\(m_{1}\),\(m_{2}\)は2つの物体の質量、\(r\)は物体間の距離です。
この式から、万有引力\(F\)は物体間の距離\(r\)の2乗に反比例することがわかります。
すなわち、距離が大きくなるほど、万有引力は小さくなります。
従って、物体Yから受ける万有引力の大きさは、物体X表面の位置によって異なります。
図1(a)のように、物体Yに面した側では万有引力が大きく、その反対側では万有引力が小さくなります。
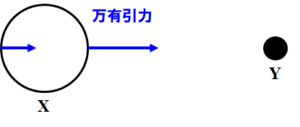
図1.(a) 位置によって万有引力が異なる
物体X上で、万有引力の大きさに差が生じると、物体Yに面した側は物体Yの方向に引っ張られて伸びます。
一方、その反対側は万有引力の影響が小さいため、物体Yに面した側の動きについていけません。
物体Yの反対側では、慣性によりその場で踏みとどまろうとする力が生じます。
その結果、物体Xは物体Yと反対の方向にも伸びます。
図1(b)で示すように、球体だった物体Xが、左右に引っ張られて楕円状に変形します。
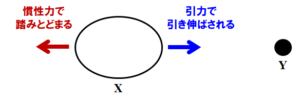
図1.(b) 物体Xにはたらく潮汐力
このような、物体Xを引き伸ばそうとする力を、「潮汐力」と呼びます。
潮汐力は、万有引力の影響下にある全ての物体にかかります。
同じ物体上での万有引力に大きな差が生じるほど、潮汐力は大きくなります。
潮汐力が非常に大きくなると、物体が引き伸ばされる力に耐えきれず、引き千切られるように破壊されます。
ブラックホールの近くで起こる「スパゲッティ化」がこれに当たります。
スパゲッティ化に関する記事はこちら。
2. 潮汐現象(潮の満ち引き)とは何か
2-1. 回転による遠心力を考慮する
地球と月は、お互いが万有引力で引き合い、回転している連星系です。
図2は、地球と月の連星系の図です。
共通重心Gを中心として、地球と月はお互いのまわりを回っています。
地球と月の共通重心Gは、地球の中心から約4600kmのところにあります。
これは、地球の半径より小さい値なので、共通重心Gは地球の内部にあることになります。

図2. 地球の月の連星系のイメージ図
回転する物体にはたらく求心力\(Fc\)についておさらいします。
万有引力と同様に、『ケプラーの法則 ~惑星が回る軌道のお話』の記事に記載したものです。
求心力\(Fc\)は以下のようになります。
$$Fc=\frac{4\pi^2m_{2}r}{T^2}$$
\(m_{2}\)は回転する物体の質量、\(T\)は回転周期です。
この式から、求心力\(Fc\)は物体間の距離\(r\)に比例することがわかります。
求心力は、回転の中心方向に向けてかかる力です。
ここで、遠心力について考えます。
求心力とは真逆で、回転の中心から外側に向けてかかる力です。
回転する物体では、遠心力は求心力\(Fc\)と釣り合うため、大きさが等しくなります。
遠心力も、物体間の距離\(r\)に比例すると考えることができます。
2-2. 地球上の各地点にかかる力
ここからは、地球表面の各地点での万有引力と遠心力の大きさを見ていきます。
図3に、地球表面の8地点における万有引力を示します。
まず、万有引力は「物体間の距離\(r\)の2乗に反比例する」だったので、月からの距離が近い地点ほど、かかる万有引力は大きくなります。
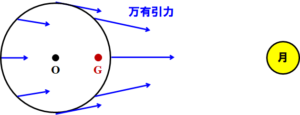
図3. 万有引力の大きさ
次に、遠心力はどうなるでしょうか。
遠心力は「物体間の距離\(r\)に比例する」だったので、連星系では共通重心Gからの距離に比例します。
図4に、図3と同じ8地点での遠心力を示します。
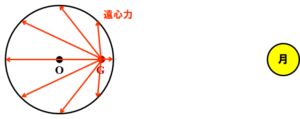
図4. 遠心力の大きさ
次に、図4の遠心力のうち、潮の満ち引きに関わる成分だけを抽出します。
図5に示すように、遠心力を地球の原点Oを経由する2つのベクトルに分解します。
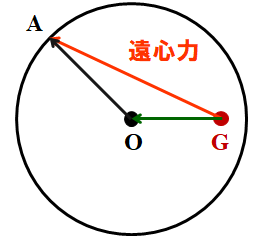
図5. 遠心力の分解
GA = GO + OA
このうち、ベクトルGOは海水に横向きの力を加え、ベクトルOAは海水を真上に押し上げる方向にはたらきます。
よって、潮の満ち引きを考える場合には、ベクトルGOのみを考えればよいのです。
図6には、8地点にかかるベクトルGOの成分を、海水を動かす遠心力として表記しました。
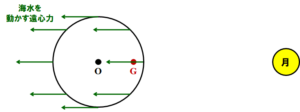
図6. 潮の満ち引きに関わる遠心力
.png)