ケプラーの法則は、17世紀初頭、ヨハネス・ケプラーによって導かれました。
たった3つの法則で、太陽のまわりを回る惑星の運動が正確にわかるのです。
ケプラーの法則
第1法則:惑星の公転軌道は、太陽を1つの焦点とする楕円になる。
第2法則:太陽と惑星を結ぶ線が、一定時間に描く面積は一定である。
第3法則:惑星の公転周期の2乗は、その惑星の太陽からの平均距離の3乗に比例する。
それでは、これら3つの法則が意味するところを見ていきましょう。
目次
1. ヨハネス・ケプラーってどんな人?
ヨハネス・ケプラーは、1571年にドイツで生まれました。
子ども時代はプロテスタントの神学校で学び、大学では牧師になるための勉強をしました。
ケプラーは、神が創った世界には、神の心に沿った調和が存在すると信じ、その調和を調べたいと考えるようになりました。
そしてケプラーは大学で、「太陽中心説」に出会います。
当時のキリスト教社会では、地球を世界の中心とする「天動説」以外はよこしまな思想とされていました。
しかしケプラーは、神の象徴である太陽こそが中心であり、その他のものは太陽のまわりを回っていると信じたのです。
ケプラーは牧師になることを辞めて、数学教師をしながら天文学や気象学、占星術などの知識を吸収していきました。
同じ頃、ティコ・ブラーエというデンマークの貴族がいました。
ティコ・ブラーエは、数十年にわたって惑星を観測し、膨大なデータを集めた人です、
1598年、ドイツで起こったプロテスタントへの迫害をきっかけに、ケプラーは故郷から追放されました。
このときケプラーは妻子を連れ、ティコ・ブラーエのもとへ避難したのです。
ケプラーはティコ・ブラーエの惑星観測を手伝い、ティコ・ブラーエの死後に膨大な観測データを引き継ぎました。
この、数十年にも及ぶ惑星の観測データから、ケプラーの法則が導かれました。
2. ケプラーの第1法則
「惑星の公転軌道は、太陽を1つの焦点とする楕円になる。」
ケプラーの時代は、真円こそが美しいとされていました。
ですからケプラーも最初は、惑星の軌道を真円として計算していました。
しかし、真円ではどうしても観測結果と合いません。
最終的に観測結果とマッチしたのが、楕円軌道だったのです。
図1で示すと、以下のようになります。
楕円には2つの焦点がありますが、そのどちらか1つに太陽が位置します。
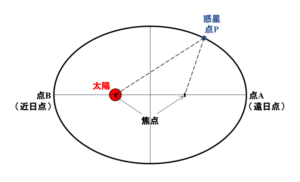
図1. 惑星が描く楕円軌道
※焦点の定義
楕円とは、ある2点からの距離の和が一定となる点で描かれた曲線のことです。
この、ある2点のことを「焦点」と呼びます。
図1中に、惑星(点P)と2つの焦点を結ぶ点線を示していますが、点Pが楕円軌道上のどこにあっても、点線の長さはいつも同じになります。
また、この定義からいうと「真円とは、2つの焦点が一致した特殊な楕円」ということができます。
豆知識➀ 遠日点と近日点(遠地点と近地点)
図1中に示した点Aを「遠日点」、点Bを「近日点」と呼びます。
文字通り、「遠日点」とは太陽と惑星の距離が最も遠くなる点のことです。
一方「近日点」では、太陽と惑星の距離が最も近くなります。
彗星など、極端に細長い楕円軌道を持つ天体では、遠日点にいるか近日点にいるかで、太陽との距離が数十倍~百倍くらい変わってきます。
ちなみに、惑星のまわりを回る衛星の軌道にも、ケプラーの第1法則は適用できます。
焦点にいるのが地球、楕円軌道を回るのが月だった場合、点Aは「遠地点」、点Bは「近地点」と呼ばれます。
豆知識② 小惑星リュウグウの軌道
2018年6月27日、JAXAの小惑星探査機「はやぶさ2」が小惑星リュウグウに到着しました。
小惑星リュウグウの公転軌道はどうなっているのでしょうか?
リュウグウの公転軌道は、地球などの惑星と比べると細長い楕円形状です。
リュウグウの遠日点は火星の軌道と重なり、近日点は地球の公転軌道より内側にあります。
つまり、地球~火星の近くを行ったり来たりしている小惑星だということです。
うっかりタイミングが合ってしまったら、地球に衝突するかもしれない天体なのです!
「PHA(潜在的に危険な小惑星)」と呼ばれる、地球に衝突する可能性が高く、かつ衝突したら地球に与える影響が大きい小惑星に分類されています。
3. ケプラーの第2法則
面積速度一定の法則ともいいます。
「太陽と惑星を結ぶ線が、一定時間に描く面積は一定である。」
では、図2を見ていきましょう。
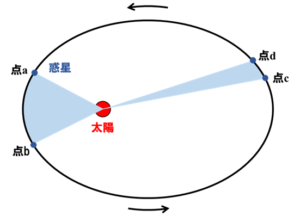
図2. 面積速度一定を示す図
ある一定時間に、惑星が楕円軌道上の点a~点bまで進んだとしましょう。
焦点の1つにいる太陽と、点a,bを線で結ぶと、水色で示したくさび型ができます。
次に、同じくある一定時間に、惑星は楕円軌道上の点c~点dに進みました。
ここでも、太陽と点c,dを線で結んだくさび型ができます。
このくさび型の面積が、惑星が楕円軌道上のどこにあろうと一定になる、というのがケプラーの第2法則です。
水色で示した面積は、いつでも等しいのです。
この法則は、何を意味するのでしょうか?
点a~点bの距離と、点c~点dの距離の違いに注目してください。
太陽から近い位置にある点a~点bの距離は長く、太陽から遠い位置にある点c~点dの距離は短くなっています。
惑星がこれらの距離を進むのにかかる時間は同じです。
つまり惑星の速さは、点a~点b間では速く、点c~点d間ではゆっくりなのです。
豆知識③ 彗星は太陽に近づくとスピードを上げる
ハレー彗星の例を見てみましょう。
ハレー彗星の遠日点は海王星の公転軌道の外側にあり、近日点は金星の公転軌道の内側にあります。
細長い楕円軌道を、およそ76年周期で一周しています。
太陽に近づくと、太陽と反対方向に尾を引く彗星の姿を観測できますが、その期間はたかだか数カ月です。
76年も待って、なぜたった数カ月しか見えないのでしょうか?
それは、ケプラーの第2法則に従って、太陽に近づいたときの彗星の速度が速くなっているからです。
地球からは見えていませんが、太陽から遠い場所では、ハレー彗星はゆっくりと進んでいるのです。
何十年も現れず、現れたと思ったらすぐに去っていく…。
不規則に感じられる彗星の動きは、実は法則どおりに安定したものなのです。
.png)